三天入门机器学习

1.1 人工智能概述

1.1.1 机器学习与人工智能深度学习

达特茅斯会议-人工智能的起点
机器学习是人工智能的一个实现途径
深度学习是机器学习的一个方法发展而来

1.1.2机器学习、深度学习能做些什么

传统预测 量化投资广告推荐
图像识别
自然语言处理 文本分类情感分析文本检测

1.2什么是机器学习

1.2.1 定义

从数据中自动分析获得模型 并利用模型对未知数据进行预测

1.2.3 数据集构成

结构：特征值+目标值

每一行数据称为样本

有些数据集可以没有目标值

1.3 机器学习算法分类

1.3.1 监督学习

目标值：类别 - 分类问题

目标值：连续型数据-回归问题

目标值：无-无监督学习

监督学习

分类k-近邻算法贝叶斯分类决策树随机森林逻辑回归

回归线性回归岭回归
无监督学习

K-MEANS

1.4 机器学习开发流程

获取数据 -> 数据处理 -> 特征工程-> 机器学习算法训练->模型 ->模型评估

1.5 学习框架和资料介绍

算法是核心数据与计算是基础

找准定位
怎么做？
1、入门
2、实战类书籍
3、机器学习 -”西瓜书”- 周志华
统计学习方法 - 李航
深度学习 - “花书”

1.5.1 机器学习库与框架

2.1 数据集

目标
- 直到数据集分为训练集和测试集
- 会使用sklearn的数据集

2.1.1可用数据集

公司内部百度

数据接口花钱

数据集

Kaggle:www.kaggle.com/datasets

UCI 数据集: http://archive.ics.uci.edu/ml/

scikit-learn: http://scikit-learn.org/stable/datasets/index.html#datasets

数据接口花钱
数据集
学习阶段可以用的数据集：
1）sklearn - 数据量小方便学习
2）kaggle 大数据竞赛平台
3）UCI

Scikit-learn工具介绍

classification ->分类

regression ->回归

clustering->聚类

dimensionality reduction ->降维

model selection ->模型选择

preprocessing ->特征工程

2.1.2 sklearn 数据集

1 scikit-learn 数据集api介绍

sklearn.datasets
- 加载获取流行的数据集
- dataset.load_*()
  - 获取小规模数据集数据包含在datasets里
- datasets.fetch_*(data_home = None)
  - 获取大规模数据集从网络上下载函数第一个参数是data_home表示数据集下载的目录默认是~/scikit_learn_data/

2 sklearn 小数据集

sklearn.datasets.load_iris()

加载并返回鸢尾花数据集
sklearn.datasets.load_boston()

加载并返回波士顿房价数据集

3 sklearn大数据集

sklearn.datasets.fetch_20newsgroups(data_home = None,subset = ‘train’)
- subset: ‘train’或者’test’ 'all’可选选择要加载的数据集
- 训练集的训练测试集的测试

4 sklearn数据集的使用

load 和 fetch 返回的数据类型databases.base.Bunch（字典格式）

1 2	`dict["key"] = values bunch.key = values`

data:特征数据数组是[n_samples *n _features]的二维numpy.ndarray数组
target:标签数组是n_samples的一维numpy.ndarray数组
DESCR:数据描述
feature_names:特征名新闻数据手写数字回归数据集没有

target_name:标签名

from sklearn.datasets import load_iris
def datasets_demo():
 # 获取数据集
 iris = load_iris()
 print("鸢尾花数据集：\n", iris)
 print("查看数据集描述：\n", iris["DESCR"])
 print("查看特征值的名字：\n",iris.feature_names)
   #150个样本 4个特征
 print("查看特征值：\n",iris.data,iris.data.shape)
 return None
if __name__ == "__main__":
   # 代码1：数据集使用
  datasets_demo()

拿到的数据是否可以全部用来训练一个模型？

2.1.3 数据集的划分

训练数据：用于训练，构建模型
测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

训练集 70% 80% 75%
测试集 30% 20% 30%
sklearn.model_selection.train_test_split(arrays, *options)
训练集特征值，测试集特征值，训练集目标值，测试集目标值
x_train x_test, y_train y_test
x 数据集的特征值
y数据集的标签值
test_size 测试集大小一般为float
random_state 随机数种子不同种子会造成不同的随机采样结果相同的种子采样结果相同

return 训练集特征值测试集特征值训练集目标值测试集目标值

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split


def datasets_demo():
    # 获取数据集
    iris = load_iris()
    print("鸢尾花数据集：\n", iris)
    print("查看数据集描述：\n", iris["DESCR"])
    print("查看特征值的名字：\n", iris.feature_names)
    # 150个样本 4个特征
    print("查看特征值：\n", iris.data, iris.data.shape)
    # 数据集划分
    x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
    print("训练集的特征值：\n", x_train, x_train.shape)

    return None


if __name__ == "__main__":
    # 代码1：数据集使用
    datasets_demo()

2.2 特征工程介绍

算法特征工程

2.2.1 为什么需要

数据与特征决定上限模型和算法只是逼近上限

2.2.2 什么是特征工程

sklearn 特征工程
pandas 数据清洗、数据处理
特征抽取/特征提取
机器学习算法 - 统计方法 - 数学公式
文本类型 -> 数值
类型 -> 数值

2.3.1 特征提取

1 将任意数据（文本、图像）转换为可用于机器学习的数字特征

注：特征值化是为了计算机更好的去理解

字典特征提取（特征离散化）
文本特征提取
图像特征提取

2 特征提取API

sklearn.feature_extraction

2.3.2 字典特征提取 -类别->one-hot编码

作用：对字典数据特征值化

sklearn.feature_extraction.DictVectorizer(sparse=True,…)
vector 数学：向量物理：矢量
矩阵 matrix 二维数组
向量 vector 一维数组
父类：转换器类

DictVectorizer.fit_transform(X):字典或者字典的迭代器返回值：返回sparse矩阵
DictVectorizer.inverse_transform(X):array数组或者sparse矩阵：返回值：转换之前的数据格式
DictVectorizer.get_feature_names_out():返回类别名称
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

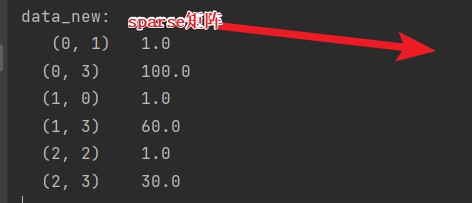
![snipaste20230717_112943](https://cdn.jsdelivr.net/gh/paipai2001/img@main/blogs/snipaste20230717_112943.jpg)

**sparse稀疏**
**将非零值->按位置表示出来**
**节省内存->提高加载效率**

![snipaste20230717_114105](https://cdn.jsdelivr.net/gh/paipai2001/img@main/blogs/snipaste20230717_114105.jpg)

```py
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
    """
    字典特征抽取
    """
    data = [{'city': '北京','temperature':100},{'city': '上海','temperature':60},{'city': '深圳','temperature':30}]
    # 1、 实例化一个转换器类
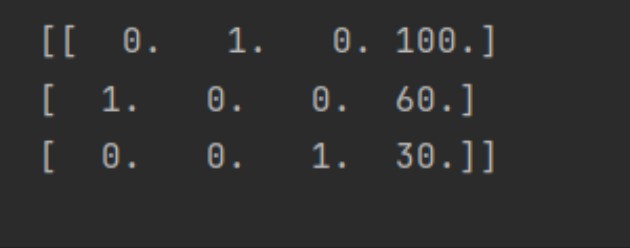
    transfer = DictVectorizer(sparse=False)
    # 2、调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    print("特征名字：\n",transfer.get_feature_names_out())
    return None
if __name__ == "__main__":
     dict_demo()

应用场景：
1.pclass, sex 数据集当中类别特征比较多
1、将数据集的特征->字典类型
2、DictVectorizer 转换

2) **本身拿到的数据就是字典类型**

2.3.3 文本特征提取

单词作为特征

句子短语单词
特征：特征词

方法1：CountVectorizer

sklearn.feature_extraction.text.CountVectorizer(stop words = [])
stop_words 停用的对最终分类没有用处
停用词表

返回词频矩阵

1
2
3

CountVectorizer.fit_transform(X):文本或者文本的迭代器返回值：返回sparse矩阵
CountVectorizer.inverse_transform(X):array数组或者sparse矩阵：返回值：转换之前的数据格式
CountVectorizer.get_feature_names_out():返回值：单词列表

案例：

from sklearn.feature_extraction.text import CountVectorizer
def count_demo():
    """
        文本特征抽取
        """
#     实例化转换器类
    transfer = CountVectorizer()
#    调用fit_transform
    data = ["life is short,i like like python", "life is too long,i dislike python"]
    data_new = transfer.fit_transform(data)
    print('data_new:\n',data_new.toarray())
    # 如果要看到二维数组的结果 在后面调用toarray()这个函数就可以啦
    return None

统计每个样本特征词出现的个数

中文转换器需要使用空格

def count_chinese_demo():
    """
    中文文本特征抽取：CountVecotrizer
    :return:
    """
    data = ["我 爱 北京 天安门", "天安门 上 太阳 升"]
    # 1、实例化一个转换器类
    transfer = CountVectorizer()

    # 2、调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new.toarray())
    print("特征名字：\n", transfer.get_feature_names())

    return None

注意：如果要调用特征名字得用实例化对象调用如果是查询具体数据用调用后得出的结果

方法2： jieba这一自动分节器

#记得导包 此处省略了
def count_chinese_demo2():
    """
    中文文本特征抽取，自动分词
    :return:
    """
    # 将中文文本进行分词
    data = ["一种还是一种今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。",
            "我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。",
            "如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]

    data_new = []
    for sent in data:
        data_new.append(cut_word(sent))
    # print(data_new)
    # 1、实例化一个转换器类
    transfer = CountVectorizer(stop_words=["一种", "所以"])

    # 2、调用fit_transform
    data_final = transfer.fit_transform(data_new)
    print("data_new:\n", data_final.toarray())
    print("特征名字：\n", transfer.get_feature_names())

    return None
    #中文分词
    def cut_word(text):
    """
    进行中文分词："我爱北京天安门" --> "我 爱 北京 天安门"
    :param text:
    :return:
    """
    return " ".join(list(jieba.cut(text)))

ps: 装包的时候一般是要进入那个路径的以电脑3.11这个版本为例

cd venv\Scripts 找到那个activate.bat 启动它才能开始安装

关键词：在某一个类别的文章中出现很多但其他类别的文章中出现很少

方法3： TfidfVectorizer

TF-IDF:评估某一字词重要程度
词频（TF）: 某一个给定的词语在一篇文章中出现的频率
逆向文档频率(IDF)：总文件数目除以包含该词语文件的数目再取以10为底的对数
TF-IDF = TF*IDF
两个词 “经济”，“非常”
1000篇文章-语料库
100篇文章 - “非常”
10篇文章 - “经济”
两篇文章
文章A(100词) : 10次“经济” TF-IDF:0.2相乘
tf:10/100 = 0.1
idf:lg 1000/10 = 2
文章B(100词) : 10次“非常” TF-IDF:0.1
tf:10/100 = 0.1
idf: log 10 1000/100 = 1
对数？
2 ^ 3 = 8
log 2 8 = 3
log 10 10 = 1

API

sklearn.feature_extraction.text.TfidVectorizer(stop_words=None,…)
- 返回词的权重矩阵
  - TfidfVectorizer.fit_transform(X):文本或者文本的迭代器返回值：返回sparse矩阵
  - TfidfVectorizer.inverse_transform(X):array数组或者sparse矩阵：返回值：转换之前的数据格- T封TfidfVectorizer.get_feature_names_out():返回值：单词列表

案例和自动分节器差不多不再重复了

2.4 特征预处理

2.4.1 定义

通过一些转换函数将特征数据转换成更适合算法模型的特征数据过程

1 包含内容

数值型数据量纲化：
- 归一化
- 标准化
  
  不同规格的数据转换成统一规格单位大小差距过大

2 特征预处理API

sklearn.preprocessing

2.4.2 归一化

1 定义

通过对原始数据进行变换把数据映射到0-1区间

2 API

sklearn.preprocessing.MinMaxScaler(feature_range = (0,1)...)
- MinMaxscalar.fit_transform(X)
  - X: numpy array 格式的数据[n_samples,n_features]
    
    返回值：转换后的形状相同的array

3 数据计算

import pandas as pd
from sklearn.preprocessing import MinMaxScaler
def minmax_demo():
    """
    归一化
    :return:
    """
    #1、获取数据
    data=pd.read_csv("dating.txt")
    data = data.iloc[:,:3]
    # 选择前三列的数据 索引方式
    print("data:\n", data)
    #2.实例化一个转换器类
    transfer = MinMaxScaler()
    #3.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)

劣处：出现异常值比如极大极小那么最终结果也会不准

本身就是依靠最大最小求值鲁棒性差精确性差

2.4.3 标准化

1 定义

原始数据进行变换把数据变换到均值为0 标准差为1

2 公式

1
2
3

(x - mean) / std
std:标准差 集中程度
mead:平均值

出现异常点也不需要担忧

方差改变较小

3 API

sklearn.preprocessing.StandardScaler(feature_range = (0,1)...)

StandardScalar.fit_transform(X)
- X: numpy array 格式的数据[n_samples,n_features]
  
  返回值：转换后的形状相同的array

4 数据计算

类似不再赘述适合大数据场景

2.5 特征降维

2.5.1 降维

ndarray

维数：嵌套的层数

0维：标量

1维：向量

2维：矩阵

二维数组

在某些限定条件下降低随机变量（特征）个数得到一组主变量

效果：要求特征与特征之间不相关

2.5.2 降维的两种方式

特征选择
主成分分析

2.5.3 什么是特征选择

1 定义

数据中包含冗余或者相关变量（特征）在原有特征中找到主要特征

2 方法

Filter(过滤式)：主要探究特征本身特点特征与特征和目标值之间关联
- 方差过滤法：低方差特征过滤（所有鸟都有爪子）
- 相关系数 - 特征与特征之间的相关程度
Embedded(嵌入式)：算法自动选择特征（特征与目标
- 决策树：信息熵信息增益
- 正则化：L1 L2
- 深度学习：卷积等

嵌入式只能讲解算法时候介绍

3 模块

sklearn.feature_selection

4 过滤式

4.1 低方差特征过滤

4.1.1 API

sklearn.feature_selection.VarianceThreshold(threshold = 0.0)

VarianceThreshold.fit_transform(X)
- X: numpy array 格式的数据[n_samples,n_features]
  
  返回值：训练集差异低于threshold的特征将被删除默认值保留所有非零方差特征

4.1.2 实例

def variance_demo():
    data = pd.read_csv("factor_returns.csv")

    data = data.iloc[:,1:-2]
    print("data:\n", data)
    transfer = VarianceThreshold()
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)

4.2 相关系数

皮尔森相关系数 pearson

公式：

4.2.3 特点

4.2.4 API

from scipy.stats import pearson
- x：
- y:

两个特征的相关性

4.2.5 股票案例

1 2	`r = pearsonr(data["pe_ratio"],data["pb_ratio"]) print("相关系数：\n",r)`

可以利用for循环输出多对

特征与特征相关性很高

选取其中一个
按一定权重加权求和
主成分分析

import matpilotlib.pyplot as plt
plt.figure(figsize = (20,8),dpi = 100)
plt.scatter(data['revenue'],data['total_expense'])
plt.show()

2.6 主成分分析

2.6.1 什么是主成分分析（PCA）

高维数据转化为低维数据舍弃原有数据创造新的变量

降低原数据复杂度

回归分析或者聚类分析

1 计算案例

五个点变成三个点二维变一维

2 API

sklearn.decomposition.PCA(n_components = None)
1
2
3
n_components 小数表示保留百分之多少的信息整数减少到多少特征
- PCA.fit_transform(X)
- 返回值：转换后制定维度的array

3 数据计算

from sklearn.decomposition import  PCA
def pca_demo():
    data = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]
    transfer = PCA(n_components=0.95)
    
    data_new = transfer.fit_transform(data)
    print("data_new=\n",data_new)
    return None

2.6.2 探究用户对物品类别的喜好细分

1 需求

用户          物品类别
user_id       aisle
1）需要将user_id和aisle放在同一个表中 - 合并
2）找到user_id和aisle - 交叉表和透视表
3）特征冗余过多 -> PCA降维

2 分析

#1.获取数据
#2.合并表
#3.找到user_id 和 aisle之间的关系
#4.PCA降维
import pandas as pd
from sklearn.decomposition import PCA
order_products = pd.read_csv("./instacart/order_products__prior.csv")
products = pd.read_csv("./instacart/products.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")
#合并aisles  products
tab1 = pd.merge(aisles,products,on=["aisle_id","aisle_id"])
tab2 = pd.merge(tab1,order_products,on=["product_id","product_id"])
tab3 = pd.merge(tab2,orders,on=["order_id","order_id"])
tab3.head()
# 交叉表
table = pd.crosstab(tab3["user_id"],tab3["aisle"])
data = table[:10000]
transfer = PCA(n_components=0.95)
data_new = transfer.fit_transform(data)
# print(data_new)
print("特征类别：\n",data_new.shape)

3.1 sklearn转换器和估计器

3.1.1 转换器

转换器调用形式

fit_transform
fit
transform

1 实例化 (实例化的是一个转换器类(Transformer))
2 调用fit_transform(对于文档建立分类词频矩阵，不能同时调用)
标准化：
    (x - mean) / std
    fit_transform()
        fit()           计算 每一列的平均值、标准差
        transform()     (x - mean) / std进行最终的转换

3.1.2 估计器estimator

在sklearn中实现算法api

流程图：

1 实例化一个estimator
2 estimator.fit(x_train, y_train) 计算
    —— 调用完毕，模型生成
3 模型评估：
    1）直接比对真实值和预测值
        y_predict = estimator.predict(x_test)
        #划分好测试集x_test
        y_test == y_predict
    2）计算准确率
        accuracy = estimator.score(x_test, y_test)

3.2 K-近邻算法 KNN

3.2.1 什么是KNN

1 原理

你的邻居来判断你的类别

如果一个样本在特征空间的k个最相似（特征空间中最邻近）的样本中大多数属于某一个类别

k = 1 容易受到异常点的影响

距离公式

两个样本的距离可以通过如下公式计算欧式距离：

曼哈顿距离绝对值距离
明可夫斯基距离

2 电影类型分析

假设有几部电影六个样本打斗镜头接吻镜头目标：类型

k = 1 爱情片
k = 2 爱情片
……
k = 6 无法确定
k = 7 动作片
k值过大 容易受到样本不均衡的影响

3 问题

如果取的电影数量不一样？会是什么结果？
结合前面约会数据需要对数据怎么样预处理？

1 2	`-无量纲化的处理 -标准化`

3.2.2 KNN API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
n_neighbors：k值 k_neighbors查询默认使用的邻居数
algorithm:{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’} 搜索邻居啥的
auto 将根据传递给fit方法选择最合适的算法

3.2.3 案例

1 数据集介绍

iris数据集

1）获取数据
2）数据集划分
3）特征工程
    标准化
4）KNN预估器流程
5）模型评估

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
    """
    用knn算法对鸢尾花数据集进行分类
    :return:
    """
    # 1）获取数据
    iris = load_iris()
    # 2）划分数据集
    x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=6)
    # 3) 特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    # 因为如果使用测试集自己的平均值会出现偏差 所以仅仅使用transform
    x_test = transfer.transform(x_test)
    # 4) KNN算法预估器
    estimator = KNeighborsClassifier()
    estimator.fit(x_train,y_train)
    # 5) 模型评估
    # 方法一：直接比对实际值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接比对真实值和预测值：\n",y_test == y_predict)
    # 方法二 ：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)
    return None
if __name__ == "__main__":
     knn_iris()

不能使用太大的数据量开销很大

3.3 模型选择与调优

3.3.1 什么是交叉验证

1 分析

2 目的

模型准确可信

3.3.2 超参数搜索-网格搜索（Grid-Search）

1
2
3

k的取值
    [1, 3, 5, 7, 9, 11]
    暴力破解

模型中有一些参数需要我们手动指定于是就可以调优

模型选择与调优API

3.3.3 鸢尾花改进

def knn_iris_gscv():
    """
    用knn算法对鸢尾花数据集进行分类 添加网格搜索和交叉验证
    :return:
    """
    # 1）获取数据
    iris = load_iris()
    # 2）划分数据集
    x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=120)
    # 3) 特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    # 因为如果使用测试集自己的平均值会出现偏差 所以仅仅使用transform
    x_test = transfer.transform(x_test)
    # 4) KNN算法预估器
    estimator = KNeighborsClassifier()
    # 加入网格搜索和交叉验证
    param_dict = {"n_neighbors": [1,3,5,7,9,11]}
    estimator = GridSearchCV(estimator,param_grid=param_dict,cv=10)
    estimator.fit(x_train,y_train)
    # 5) 模型评估
    # 方法一：直接比对实际值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接比对真实值和预测值：\n",y_test == y_predict)
    # 方法二 ：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)
    # 最佳参数： best_params_
    print("最佳参数：\n",estimator.best_params_)
    # 最佳结果： best_score_
    print("最佳结果：\n", estimator.best_score_)
    # 最佳估计器： best_estimator_
    print("最佳估计器：\n", estimator.best_estimator_)
    # 交叉验证结果： cv_results_
    print("交叉验证结果：\n", estimator.cv_results_)

    return None

3.3.4 预测facebook签到位置

1 数据集介绍

row_id: 索引（无意义）
x y:（人所在的位置）
accuracy:（定位的准确度）
time:（在哪个时间在定位位置）
place_id；用户将要签到的位置

流程分析：
    1）获取数据
    2）数据处理
    目的：
        特征值 x
        目标值 y
        a.缩小数据范围
          2 < x < 2.5
          1.0 < y < 1.5
        b.time -> 年月日时分秒
        c.过滤签到次数少的地点
        数据集划分
     3）特征工程：标准化
     4）KNN算法预估流程
     5）模型选择与调优
     6）模型评估

2 实际操作

# 3) 特征工程：标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
# 因为如果使用测试集自己的平均值会出现偏差 所以仅仅使用transform
x_test = transfer.transform(x_test)
# 4) KNN算法预估器
estimator = KNeighborsClassifier()
# 加入网格搜索和交叉验证
param_dict = {"n_neighbors": [3,5,7,9]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
estimator.fit(x_train,y_train)
# 5) 模型评估
# 方法一：直接比对实际值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值：\n",y_test == y_predict)
# 方法二 ：计算准确率
score = estimator.score(x_test,y_test)
print("准确率为：\n",score)
# 最佳参数： best_params_
print("最佳参数：\n",estimator.best_params_)
# 最佳结果： best_score_
print("最佳结果：\n", estimator.best_score_)
# 最佳估计器： best_estimator_
print("最佳估计器：\n", estimator.best_estimator_)
# 交叉验证结果： cv_results_
print("交叉验证结果：\n", estimator.cv_results_)

结果：

y_predict:
 [1732563460 4642646293 7038685199 ... 9386144778 1380291167 3974542317]
直接比对真实值和预测值：
 10123260    False
16370269     True
8987212     False
25350732     True
2350188     False
27448389    False
18266407     True
20832425    False
20061648    False
9937274      True
22854526     True
9059450     False
24798827    False
5357941     False
21559497    False
17593468    False
3565205     False
1525691     False
24745125     True
17098577     True
24135559     True
24747751    False
3562966     False
8754665     False
4945947     False
19454562     True
124153      False
16592306    False
19493243    False
14946077     True
            ...  
2576728      True
17692961     True
1354061     False
8557538     False
26498264    False
15611307     True
19636821     True
7009739     False
14926961     True
8277291     False
7855506      True
20458273     True
26659503    False
12580447    False
6001349     False
8852544      True
12590771    False
6977831     False
22776654    False
25406749    False
3223869     False
12451110    False
18903770    False
27155003    False
7637819      True
480605      False
11920745    False
2818989     False
11329355    False
17936911    False
Name: place_id, Length: 20228, dtype: bool
准确率为：
 0.3661755981807396
最佳参数：
 {'n_neighbors': 7}
最佳结果：
 0.33317952605385454
最佳估计器：
 KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=7, p=2,
           weights='uniform')

3.4 朴素贝叶斯算法

3.4.1 什么是朴素贝叶斯算法

3.4.2 概率基础

3.4.3 联合概率条件概率相互独立

3.4.4 贝叶斯公式

1 公式

注：w为给定文档的特征值（频数估计预测文档提供）c为文档类别

 联合概率：包含多个条件，且所有条件同时成立的概率
    P(程序员, 匀称) P(程序员, 超重|喜欢)
    P(A, B)
    条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
    P(程序员|喜欢) P(程序员, 超重|喜欢)
    P(A|B)
    相互独立:
        P(A, B) = P(A)P(B) <=> 事件A与事件B相互独立
朴素？
    假设：特征与特征之间是相互独立
朴素贝叶斯算法：
    朴素 + 贝叶斯
应用场景：
    文本分类
    单词作为特征
拉普拉斯平滑系数

2 文章分类计算

P© = 3/4 属于china类的概率

3 拉普拉斯平滑系数

防止计算出的分类概率为 0

P(F1|C) =(Ni+a)/N+am

a 为指定系数一般为1 m为训练文档中统计出的特征词个数

3.4.5 API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数

3.4.6 案例：20个新闻组

1）获取数据
2）划分数据集
3）特征工程
    文本特征抽取
    TFIDF 单词抽取
4）朴素贝叶斯预估器流程
5）模型评估

代码：

def news_demo():
    """
    用朴素贝叶斯对新闻分类
    :return:
    """
    #1 获取数据
    news = fetch_20newsgroups(subset="all")
    #2 划分数据集
    x_train,x_test,y_train,y_test = train_test_split(news.data,news.target)
    #3 特征工程
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    #4 朴素贝叶斯算法
    estimator = MultinomialNB()
    estimator.fit(x_train,y_train)
    #5
    # 方法一：直接比对实际值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二 ：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)
    return None

3.4.7 总结

优点：
    对缺失数据不太敏感，算法也比较简单，常用于文本分类。
    分类准确度高，速度快
缺点：
    由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

3.5 决策树

3.5.1 认识决策树

1 2	`如何高效的进行决策？特征的先后顺序`

if-else

3.5.2 决策树原理详解

1
2
3

已知 四个特征值 预测 是否贷款给某个人
先看房子，再工作 -> 是否贷款 只看了两个特征
年龄，信贷情况，工作 看了三个特征

问题：如何对这些客户进行分类预测？

1 原理

信息熵信息增益

2 信息熵的定义信息的衡量 - 信息量 - 信息熵

H的专业术语称为信息熵单位为比特

$H(X) = -$ P(xi)lobb(P(xi))的和

香农：消除随机不定性的东西
小明 年龄 “我今年18岁” - 信息
小华 ”小明明年19岁” - 不是信息
  bit
g(D,A) = H(D) - 条件熵H(D|A)

结果是0.971

3 决策树的划分依据之一——信息增益

定义与公式

特征A对训练集D的信息增益g(D,A) 定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵的H(D|A)之差：

g(D,A) = H(D) - 条件熵H(D|A)

4 其他依据

ID3
- 信息增益最大的准则
C4.5
- 信息增益比最大的准则
CART
- 分类树：基尼系数最小的准则在sklearn中可以划分的默认原则
- 优势：划分更加细致

3.5.3 决策树API

class sklearn.tree.DecisionTreeClassifier(criterion = 'gini',
max_depth = None,random_state = None)
- 决策树分类器
- criterion:默认是‘gini’系数可以选择信息增益的熵’entropy’
- max_depth:树的深度大小
- random_state:随机数种子

鸢尾花的例子：

def decision_iris():
    #1)获取数据集
    iris = load_iris()
    #2）划分数据集
    x_train,x_test,y_train,y_test  = train_test_split(iris.data,iris.target,random_state=22)
    #3）决策树
    estimator = DecisionTreeClassifier(criterion='entropy')
    estimator.fit(x_train,y_train)
    #4）
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二 ：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)
    return None

没有免费的午餐：总是想找到一个算法一劳永逸

样本数目太少了

3.5.4 案例：泰坦尼克号乘客生存预测

泰坦尼克号数据

1 乘坐班是指乘客班（1,2,3）社会经济阶层的代表

2 其中age数据存在缺失

数据：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

分析步骤

流程分析：
    特征值 目标值
    1）获取数据
    2）数据处理
        缺失值处理
        特征值 -> 字典类型
    3）准备好特征值 目标值
    4）划分数据集
    5）特征工程：字典特征抽取
    6）决策树预估器流程
    7）模型评估

选择若干个重要的特征

from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier,export_graphviz
def decision_tree():
    #获取数据
    data = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
    #筛选特征值和目标值
    x = data[['pclass', 'age', 'sex', 'name', 'room']]
    y = data['survived']
    #2.数据处理 1）处理缺失值 填补先索引 填补平均值 
    x['age'].fillna(x['age'].mean(), inplace=True)#fillna(替换的值，inplace表示替换默认为False）
    #划分训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
    #特征工程（类别信息进行ONE-HOT编码）准换成字典to_dict
    Dict = DictVectorizer(sparse=False)#对字典数据进行特征值化,不按照sparse矩阵展示
    x_train = Dict.fit_transform(x_train.to_dict(orient="records"))#to_dict将数据转换成字典，orient="record"默认按照行进行
    x_test = Dict.fit_transform(x_test.to_dict(orient="records"))
    #决策树预测
    dt = DecisionTreeClassifier(max_depth=5)
    dt.fit(x_train, y_train)
    #准确率评价
    print("准确率为", dt.score(x_test, y_test))
    #导出决策树结构
    export_graphviz(dt, out_file='./tree.dot', feature_names=['pclass', 'age', 'sex', 'name', 'room'])
    return None
if __name__== "__main__":
    decision_tree()

3.5.3 决策树可视化

1 保存树的结构到dot文件

sklearn.tree.export_graphviz()该函数可以导出DOT格式
- tree.export_graphviz(estimator, out_file = “tree.dot”,feature_names = [‘’,'])

export_graphviz(dc, out_file = "./tree.dot",feature_names = ['age','plcass=1'])

2 网站结构

http://webgraphviz.com/

3.5.6 总结

优点：
    可视化 - 可解释能力强
缺点：
    容易产生过拟合

3.6 集成学习方法之随机森林

3.6.1 什么是集成学习方法

集成学习通过建立几个模型组合的来解决单一预测问题它的工作原理是生成多个分类器/模型各自独立学习和作出预测

因此优于任何一个单分类作出预测

3.6.2 什么是随机森林

在机器学习中 随机森林是一个包含多个决策树的分类器 并且输出类别是由个别树输出的类别的众数而定

假如训练了5个树有四个树结果为true 1个树结果为false 最终投票结果为true

3.6.3 随机森林原理过程

训练集：
N个样本
特征值 目标值
M个特征
随机
    两个随机
        训练集随机 - N个样本中随机有放回的抽样N个

学习算法根据下列算法建造每棵树：

用N来表示训练用例（样本）的个数 M表示特征数目
- 1 一次随机选择一个样本重复N次
- 2 随机选出m个特征建立决策树

采用bootstrap抽样

 bootstrap 随机有放回抽样
        [1, 2, 3, 4, 5]
        新的树的训练集
        [2, 2, 3, 1, 5]
    特征随机 - 从M个特征中随机抽取m个特征
        M >> m
        降维

3.6.4 API

class sklearn.ensemble.RandomForestClassifier(n_estimator = 10,critetion = ‘gini’,
max_depth = None;bootstrap = True,random_state = None,min_samples_split = 2)

3.6.5 随机森林预测案例

5,8,15

超参数调优：

1 2	`gc = GridSearchCV(rf,param_grid = param,cv = 2) gc.fit(x_train,y_train)`

3.6.6 总结

1 2	`能够有效地运行在大数据集上，处理具有高维特征的输入样本，而且不需要降维`

4 回归与聚类算法

回归和聚类
线性回归
欠拟合与过拟合
岭回归
分类算法：逻辑回归
模型保存与加载
无监督学习 K-means算法

4.1线性回归

4.1.1 线性回归的内容

1 2	`回归问题：目标值 - 连续型的数据`

房价预测
销售额度预测
金融：贷款额度预测、利用线性回归

2 什么是线性回归

利用回归方程对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式

单变量回归多变量回归

1
2
3

    线性关系
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b（偏置）
  = wTx（逆） + b

w x 理解成矩阵

数据挖掘基础
y = kx + b
y = w1x1 + w2x2 + b
y = 0.7x1 + 0.3x2
期末成绩：0.7×考试成绩+0.3×平时成绩

广义线性模型
    非线性关系？
    线性模型
        自变量一次
         y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
        参数一次
         y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b
    线性关系&线性模型
    线性关系一定是线性模型
    线性模型不一定是线性关系

4.1.2 线性回归的损失和优化原理（理解记忆）

目标：求模型参数
模型参数能够使得预测准确
真实关系：真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
随意假定：预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率

不断更新权重与损失两者差距越小越接近

如何衡量差距？
损失函数/cost/成本函数/目标函数

最小二乘法

1 损失函数

2 优化算法

如何去求模型中的W 使得损失最小？

直接求解w

拓展：
1)
    y = ax^2 + bx + c
    y' = 2ax + b = 0
    x = - b / 2a
2)
    a * b = 1
        b = 1 / a = a ^ -1
    A * B = E
    单位矩阵
    [[1, 0, 0],
    [0, 1, 0],
    [0, 0, 1]]
    B = A ^ -1

梯度下降

4.1.3 线性回归API

sklearn.linear_model.LinearRegression(fit_intercept = True)
sklearn.linear_model.SGDRegressor(loss = "squared_loss",fit_intercept = True,learing_rate = 'invscaling',eta0 = 0.01)
不加上偏置只能过原点

loss:损失函数
学习率：步长

4.1.4 波士顿房价预测

流程：
    1）获取数据集
    2）划分数据集
    3）特征工程：
        无量纲化 - 标准化
    4）预估器流程
        fit() --> 模型
        coef_ intercept_
    5）模型评估

代码：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
def linear1():
    """

    :return:
    """
    #1获取数据集
    boston = load_boston()
    #2 划分数据集
    x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,random_state=22)
    #3 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    #4 模型
    estimator = LinearRegression()
    estimator1 = SGDRegressor()
    estimator.fit(x_train,y_train)
    #5 评估模型
    print("权重系数为：\n",estimator.coef_)
    print("偏置为：\n",estimator.intercept_)
if __name__ == "__main__":
    print()
    #自从1.2 版本后波士顿数据集给移出去了

1 回归性能评估

均方误差评价机制：

1
2
3

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error

模型评估：

y_predict = estimator.predict(x_test)
print('预测房价为：\n',y_predict)
error = mean_squared_error(y_test,y_predict)
print("正规方程的均方误差为:\n",error)

值越小越好表示误差程度

2 对比

梯度下降	正规方程
需要选择学习率	NO
需要迭代求解	一次求解
特征数目较大可以使用	计算方程时间复杂度高

选择：
- 小规模数据：
  - LinearRegression(不能解决拟合问题)
  - 岭回归
- 大规模数据：SGDRegressor

GD SGD SAG

4.2 欠拟合和过拟合

训练集上没事但测试集表现很差

那估计就是过拟合

4.2.1 什么是过拟合与欠拟合

欠拟合学习到的特征太少了
过拟合学习到的特征太多了

定义

过拟合：一个假设在训练集上能够获得比其他假设更好的拟合但在测试集上不能很好拟合数据所以出现过拟合模型过于复杂
欠拟合：一个假设在训练集和测试集都不能很好的拟合数据模型过简单

4.2.2 原因以及解决办法

欠拟合原因以及解决办法
- 原因：学习到数据的特征过少
- 解决办法：增加数据的特征数量
过拟合原因以及解决方法
- 原因：原始特征过多存在一些嘈杂特征模型过于复杂是因为模型尝试去兼顾每个测试数据点
- 解决办法：正则化
减少高次项特征的影响

1 正则化

L2正则化（常用）
- 让一些W更小接近0 那么就可以削弱了

L1
损失函数 + λ惩罚项
LASSO
L2 更常用
损失函数 + λ惩罚项
Ridge - 岭回归

4.3 岭回归

4.3.1 带有L2正则化的线性回归——岭回归

算法建立回归方程的时候加上正则化解决过拟合的效果

1 API

Ridge方法相当于SGDRegressor(penalty = ‘l2’,loss = ‘squared_loss’),只不过这个实现了一个普通的梯度下降学习

2 观察正则化程度的变化对结果的影响

3 波士顿房价预测

def linear3():
    """
    岭回归对波士顿房价预测
    :return:
    """
    #1获取数据集
    boston = load_boston()
    print("特征数量:\n",boston.data.shape)
    #2 划分数据集
    x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,random_state=22)
    #3 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    #4 模型
    estimator = Ridge(alpha = 0.5,max_iter = 10000)
    estimator.fit(x_train,y_train)
    #5 评估模型
    print("权重系数为：\n",estimator.coef_)
    print("偏置为：\n",estimator.intercept_)
    #6 模型评估
    y_predict = estimator.predict(x_test)
    print('预测房价为：\n',y_predict)
    error = mean_squared_error(y_test,y_predict)
    print("正规方程的均方误差为:\n",error)

4.4 分类算法-逻辑回归与二分类

4.4.1 逻辑回归的应用场景

广告点击率
是否为垃圾邮件
是否患病
金融诈骗
虚假账号

正例 / 反例

4.4.2 逻辑回归原理

1 输入

逻辑回归的输入就是一个线性回归的结果

2 激活函数

sigmoid函数结果代替x
1
1/(1 + e^(-x))

分析
- 回归的结果输入到sigmoid函数当中
- 输出结果：[0,1]区间中的一个概率值默认0.5为阈值

假设函数/线性模型
    1/(1 + e^(-(w1x1 + w2x2 + w3x3 + …… + wnxn + b)))
损失函数
    逻辑回归的真实值/预测值 是否属于某个类别
    对数似然损失
    log 2 x
优化损失
    梯度下降

3 损失以及优化

1 优化

逻辑回归的损失对数似然损失 y为真实值

2 优化

同样使用梯度下降优化算法去减少损失函数得知这样去更新逻辑回归前面对应算法的权重参数提升原本属于1 类别的概率降低原本是0 的概率

4.4.3 逻辑回归API

sklearn.linear_model.LogisticRegression(solver = 'liblinear',penalty = 'l2',C=1.0)
solver:优化求解方式
sag:根据数据集自动选择 随机平均梯度下降
penalty:正则化的种类
C:正则化力度
1
2
3
4
5
6
7

> 默认将类别数量少的当做正例

### 4.4.4 案例：癌症分类预测

- https://archive.ics.uci.edu/ml/machine-learing-databases/


恶性 - 正例
      流程分析：
          1）获取数据
              读取的时候加上names
          2）数据处理
              处理缺失值
          3）数据集划分
          4）特征工程：
              无量纲化处理-标准化
          5）逻辑回归预估器
          6）模型评估

1
2
3


- 代码：

def logisticregression():
“”"
逻辑回归进行癌症预测
:return: None
“”"
# 1、读取数据，处理缺失值以及标准化
column_name = [‘Sample code number’, ‘Clump Thickness’, ‘Uniformity of Cell Size’, ‘Uniformity of Cell Shape’,
‘Marginal Adhesion’, ‘Single Epithelial Cell Size’, ‘Bare Nuclei’, ‘Bland Chromatin’,
‘Normal Nucleoli’, ‘Mitoses’, ‘Class’]

  data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                     names=column_name)

  # 删除缺失值
  data = data.replace(to_replace='?', value=np.nan)

  data = data.dropna()

  # 取出特征值
  x = data[column_name[1:10]]

  y = data[column_name[10]]

  # 分割数据集
  x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

  # 进行标准化
  std = StandardScaler()

  x_train = std.fit_transform(x_train)

  x_test = std.transform(x_test)

  # 使用逻辑回归
  lr = LogisticRegression()

  lr.fit(x_train, y_train)

  print("得出来的权重：", lr.coef_)

  # 预测类别
  print("预测的类别：", lr.predict(x_test))

  # 得出准确率
  print("预测的准确率:", lr.score(x_test, y_test))
  return None


  ### 5 分类的评估方法

  ### 1 精确率

  #### 1 混淆矩阵

  在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

  ![snipaste20230721_190811](D:\_xpl2022\Desktop\markdown\picture\snipaste20230721_190811.jpg)

#### 2 精确率与召回率

- 精确率：预测结果为正例样本中真实为正例的比例（了解）
- 召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）

还有其他的评估标准，F1-score，反映了模型的稳健型 越高越好

![snipaste20230722_145347](D:\_xpl2022\Desktop\markdown\picture\snipaste20230722_145347.jpg)

#### 3 分类评估API

- sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
- - y_true：真实目标值
  - y_pred：估计器预测目标值
  - labels:指定类别对应的数字 
  - target_names：目标类别名称 需要知道真实值和目标值对应的字符串传进来
  - return：每个类别精确率与召回率

`print("精确率和召回率为：", classification_report(y_test, lr.predict(x_test), labels=[2, 4], target_names=['良性', '恶性']))`

**假设这样一个情况，如果99个样本癌症，1个样本非癌症，不管怎样我全都预测正例(默认癌症为正例),准确率就为99%但是这样效果并不好，这就是样本不均衡下的评估问题**

很不负责任

准确率：99%

召回率 99/99

精确率： 99%

F1-score：99.497

#### 问题：如何衡量样本不均衡下的评估？

### 4.4.5 ROC曲线与AUC指标

#### 5.2.1 知道TPR与FPR

- TPR = TP / (TP + FN)-召回率
  - 所有真实类别为1的样本中，预测类别为1的比例
- FPR = FP / (FP + FN)
  - 所有真实类别为0的样本中，预测类别为1的比例

#### 5.2.2 ROC曲线

- ROC曲线的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5（曲线和xy轴围成的面积）

![snipaste20230722_150027](D:\_xpl2022\Desktop\markdown\picture\snipaste20230722_150027.jpg)

#### 5.2.3AUC指标

- AUC的概率意义是随机取一对正负样本，正样本得分大于负样本的概率
- AUC的最小值为0.5，最大值为1，取值越高越好
- **AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。**
- **0.5<AUC<1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。**

> **最终AUC的范围在[0.5, 1]之间，并且越接近1越好**

#### 5.2.4 AUC计算API

- from sklearn.metrics import roc_auc_score
  - sklearn.metrics.roc_auc_score(y_true, y_score)
    - 计算ROC曲线面积，即AUC值
    - y_true:每个样本的真实类别，必须为0(反例),1(正例)标记
    - y_score:每个样本预测的概率值 预测得分 正类的估计概率 置信值 或者分类器方法的返回值

0.5~1之间，越接近于1约好因为y_true数值有要求则大于2.5为1 否则为0

y_test = np.where(y_test > 2.5, 1,0)
print(“AUC指标：”, roc_auc_score(y_test, lr.predict(x_test)))


#### 5.2.5、总结

- AUC只能用来评价二分类
- AUC非常适合评价样本不平衡中的分类器性能

## 4.5 模型保存和加载

### 4.5.1 sklearn模型的保存和加载API

- from sklearn.externals import joblib
  - 保存：joblib.dump(rf, 'test.pkl')
  - 第二个是路径 后缀为pkl
  - 加载：estimator = joblib.load('test.pkl')

### 4.5.2  线性回归的模型保存加载案例

- 保存

```python
# 使用线性模型进行预测
# 使用正规方程求解
lr = LinearRegression()
# 此时在干什么？
lr.fit(x_train, y_train)
# 保存训练完结束的模型
joblib.dump(lr, "test.pkl")

加载

1
2
3

# 通过已有的模型去预测房价
model = joblib.load("test.pkl")
print("从文件加载进来的模型预测房价的结果：", std_y.inverse_transform(model.predict(x_test)))

说到这个 joblib这个模块自从sklearn升级后给剔除成为一个独立的包导入是：

import joblib

4.6 无监督学习-K-means算法

4.6.1 什么是无监督学习

没有目标值

一家广告平台需要根据相似的人口学特征和购买习惯将美国人口分成不同的小组，以便广告客户可以通过有关联的广告接触到他们的目标客户。
Airbnb 需要将自己的房屋清单分组成不同的社区，以便用户能更轻松地查阅这些清单。
一个数据科学团队需要降低一个大型数据集的维度的数量，以便简化建模和降低文件大小。

我们可以怎样最有用地对其进行归纳和分组？我们可以怎样以一种压缩格式有效地表征数据？这都是无监督学习的目标，之所以称之为无监督，是因为这是从无标签的数据开始学习的。

4.6.2 无监督学习包含算法

聚类
- K-means(K均值聚类)
降维
- PCA

4.6.3 k-means原理

我们先来看一下一个K-means的聚类效果图

K-means聚类步骤

1、随机设置K个特征空间内的点作为初始的聚类中心（随机找K个点做中心）
2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别
3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）
4、如果计算得出的新中心点与原中心点一样，那么结束，否则重新进行第二步过程

我们以一张图来解释效果

K-超参数

1）看需求

2）网格搜索调节K值

K-means API

sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
- k-means聚类
- n_clusters:开始的聚类中心数量 K的值
- init:初始化方法，默认为’k-means ++’
- labels_:默认标记的类型，可以和真实值比较（不是值比较）

4.6.5 案例：k-means对Instacart Market用户聚类

5.1 分析

1、降维之后的数据
2、k-means聚类
3、聚类结果显示

5.2 代码

# 取500个用户进行测试
cust = data[:500]
km = KMeans(n_clusters=4)
km.fit(cust)
pre = km.predict(cust)

问题：如何去评估聚类的效果呢？

4.6.6 Kmeans 性能评估指标

6.1 轮廓系数

高内聚低耦合

注：对于每个点i 为已聚类数据中的样本，b_i 为i 到其它族群的所有样本的距离最小值，a_i 为i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值

6.2 轮廓系数值分析

分析过程（我们以一个蓝1点为例）
- 1、计算出蓝1离本身族群所有点的距离的平均值a_i
- 2、蓝1到其它两个族群的距离计算出平均值红平均，绿平均，取最小的那个距离作为b_i
- 根据公式：极端值考虑：如果b_i >>a_i: 那么公式结果趋近于1；如果a_i>>>b_i: 那么公式结果趋近于-1

6.3 结论

如果b_i>>a_i:趋近于1效果越好， b_i<<a_i:趋近于-1，效果不好。轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优。

6.4 轮廓系数 API

sklearn.metrics.silhouette_score(X, labels)
- 计算所有样本的平均轮廓系数
- X：特征值
- labels：被聚类标记的目标值

6.5 用户聚类结果评估

1
2
3

silhouette_score(cust, pre)
cust-data_new
pre - y_predict

7、K-means总结

特点分析：采用迭代式算法，直观易懂并且非常实用
缺点：容易收敛到局部最优解(多次聚类)

注意：聚类一般做在分类之前

三天入门机器学习

1.1 人工智能概述

1.1.1 机器学习与人工智能 深度学习

1.1.2机器学习、深度学习能做些什么

1.2什么是机器学习

1.2.1 定义

1.2.3 数据集构成

1.3 机器学习算法分类

1.3.1 监督学习

1.4 机器学习开发流程

1.5 学习框架和资料介绍

1.5.1 机器学习库与框架

2.1 数据集

2.1.1可用数据集

Scikit-learn工具介绍

2.1.2 sklearn 数据集

1 scikit-learn 数据集api介绍

2 sklearn 小数据集

3 sklearn大数据集

4 sklearn数据集的使用

2.1.3 数据集的划分

2.2 特征工程介绍

2.2.1 为什么需要

2.2.2 什么是特征工程

2.3.1 特征提取

1 将任意数据（文本、图像）转换为可用于机器学习的数字特征

2 特征提取API

2.3.2 字典特征提取 -类别->one-hot编码

2.3.3 文本特征提取

方法1：CountVectorizer

方法2： jieba这一自动分节器

方法3： TfidfVectorizer

API

2.4 特征预处理

2.4.1 定义

1 包含内容

2 特征预处理API

2.4.2 归一化

1 定义

2 API

3 数据计算

2.4.3 标准化

1 定义

2 公式

3 API

4 数据计算

2.5 特征降维

2.5.1 降维

2.5.2 降维的两种方式

2.5.3 什么是特征选择

1 定义

2 方法

3 模块

4 过滤式

4.1 低方差特征过滤

4.1.1 API

4.1.2 实例

4.2 相关系数

4.2.3 特点

4.2.4 API

4.2.5 股票案例

2.6 主成分分析

2.6.1 什么是主成分分析（PCA）

1 计算案例

2 API

3 数据计算

2.6.2 探究用户对物品类别的喜好细分

1 需求

2 分析

3.1 sklearn转换器和估计器

3.1.1 转换器

3.1.2 估计器estimator

3.2 K-近邻算法 KNN

3.2.1 什么是KNN

1 原理

2 电影类型分析

3 问题

3.2.2 KNN API

3.2.3 案例

1 数据集介绍

1.1.1 机器学习与人工智能深度学习

3.4.3 联合概率条件概率相互独立

2 信息熵的定义信息的衡量 - 信息量 - 信息熵

1 乘坐班是指乘客班（1,2,3）社会经济阶层的代表

2 观察正则化程度的变化对结果的影响